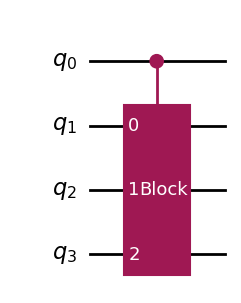
Controlled circuit blocks
A controlled circuit block is an arbitrarily complex block of quantum operations that can be switched on or off, in its entirety, using a control bit. This is a fundamentally important circuit element, as it enables you to implement if/then logic and conditionalize any kind of operation in your circuits.
Controlled gates
Controlled gates are inherently useful in quantum circuits as they enable you to apply Boolean logic. For example, using a CX gate (CNOT gate) you can implement the logic: if qubit 0 is 1, apply the Pauli X gate to qubit 1. Out of the box, Qiskit provides a variety of controlled gates for common single-qubit operations (see Methods to add standard instructions in the IBM Qiskit documentation).
The following example shows all of the built-in controlled gates provided by Qiskit at the time of writing.
from qiskit import QuantumCircuit
import numpy
circ = QuantumCircuit(3)
circ.cx(0, 1)
circ.cy(0, 1)
circ.cz(0, 1)
circ.crx(numpy.pi/4.0, 0, 1)
circ.cry(numpy.pi/4.0, 0, 1)
circ.crz(numpy.pi/4.0, 0, 1)
circ.cu(numpy.pi/4.0, 0.0, 0.0, 0.0, 0, 1)
circ.ch(0, 1)
circ.cp(numpy.pi/4.0, 0, 1)
circ.cs(0, 1)
circ.csdg(0, 1)
circ.csx(0, 1)
circ.cswap(0, 1, 2)
circ.ccx(0, 1, 2)
circ.ccz(0, 1, 2)
circ.draw(output='mpl')
Custom controlled circuit
As you start to implement more complex quantum circuits, you will quickly find yourself in a situation where you want to conditionalize a more complex operation. You might start to wonder: what are the limits to implementing controlled gates? Can you apply a control bit to any quantum operation? The answer is yes and the Qiskit library provides a simple way of adding a control bit to any block of quantum operations.
To implement a custom controlled circuit, follow these steps:
-
Create a circuit object (sub-circuit) and define all of the operations for the controlled circuit on this circuit.
-
Convert this sub-circuit to a gate, by invoking the
to_gate()method. -
Add a control bit to the gate, by invoking the
control()method.
Note: The control() method takes an integer argument that specifies
the number of control bits to add.
The following code example shows how to do this.
# Create the sub-circuit, which we will convert into a controlled block
subcirc = QuantumCircuit(3, name='Block')
subcirc.h(0)
subcirc.h(1)
subcirc.h(2)
subcirc.swap(0, 1)
subcirc.cp(numpy.pi/3.0, 1, 2)
controlled_gate = subcirc.to_gate().control(1)
# Create the main circuit
circ = QuantumCircuit(4)
circ.append(controlled_gate, [0, 1, 2, 3])
circ.draw(output='mpl')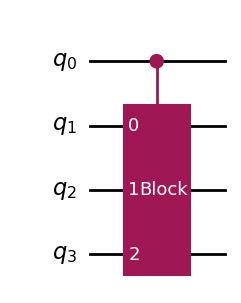
Implementation of custom controlled circuit
Now we know how to add a control bit (or bits) to an arbitrary quantum gate, you might start to wonder how this is implemented. Fortunately, as Qiskit has an open source code base, the answer to this question can be found by searching the code base.
It turns out that the control logic is implemented by the
qiskit.circuit.add_control()
method, which gives an outline of the implementation strategy in the
help text, as follows:
# This code is part of Qiskit.
#
# (C) Copyright IBM 2017, 2019.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.
"""Add control to operation if supported."""
from __future__ import annotations
from qiskit.circuit.exceptions import CircuitError
from qiskit.circuit.library import UnitaryGate
from qiskit.transpiler import PassManager
from qiskit.transpiler.passes.basis import BasisTranslator, UnrollCustomDefinitions
from qiskit.circuit.equivalence_library import SessionEquivalenceLibrary as sel
from . import ControlledGate, Gate, QuantumRegister, QuantumCircuit
from ._utils import _ctrl_state_to_int
def add_control(
operation: Gate | ControlledGate,
num_ctrl_qubits: int,
label: str | None,
ctrl_state: str | int | None,
) -> ControlledGate:
"""For standard gates, if the controlled version already exists in the
library, it will be returned (e.g. XGate.control() = CnotGate().
For more generic gates, this method implements the controlled
version by first decomposing into the ['u1', 'u3', 'cx'] basis, then
controlling each gate in the decomposition.
Open controls are implemented by conjugating the control line with
X gates. Adds num_ctrl_qubits controls to operation.
This function is meant to be called from the
:method:`qiskit.circuit.gate.Gate.control()` method.
Args:
operation: The operation to be controlled.
num_ctrl_qubits: The number of controls to add to gate.
label: An optional gate label.
ctrl_state: The control state in decimal or as a bitstring
(e.g. '111'). If specified as a bitstring the length
must equal num_ctrl_qubits, MSB on left. If None, use
2**num_ctrl_qubits-1.
Returns:
Controlled version of gate.
"""
if isinstance(operation, UnitaryGate):
# attempt decomposition
operation._define()
cgate = control(operation, num_ctrl_qubits=num_ctrl_qubits, label=label, ctrl_state=ctrl_state)
if operation.label is not None:
cgate.base_gate = cgate.base_gate.to_mutable()
cgate.base_gate.label = operation.label
return cgateTo paraphrase the help text, essentially what the algorithm is doing is decomposing the sub-circuit into its constituent gates and then applying the control bit to each of the constituent gates. This strategy is simple but ingenious, as it has multiple advantages:
-
It does not introduce any entanglement with ancillary bits.
-
It is a completely general algorithm.
-
It is easy to implement.
Multiple control bits
Another important feature of controlled gates is the ability to add multiple control bits. Essentially, in this case, the control bits are combined using AND logic, as in:
if (bit 0 AND bit 1 AND bit 2) then apply Gate
To generate a multi-controlled gate in Qiskit, invoke the control()
method on the gate, passing the number of required control bits as an
argument to the control() method, for example:
# Create a multi-controlled gate
mc_gate = subcirc.to_gate().control(3)
# Create the main circuit
circ = QuantumCircuit(6)
circ.append(mc_gate, [0, 1, 2, 3, 4, 5])
circ.draw(output='mpl')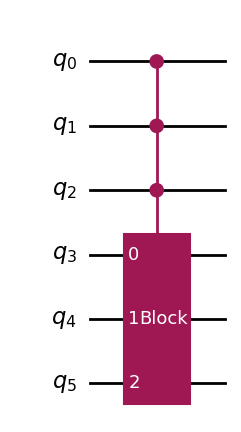
When it comes to implementing multiple controls on a gate, the simplest approach is to use a so-called V-chain. Noting that the control bits are effectively combined using classical AND logic (bit 0 AND bit 1 AND bit 2), we can use the quantum equivalent of the AND gate (the CCX or Toffoli gate) to implement the classical logic that combines the control bits with AND logic.
The following code example shows how to apply three control bits to a Hadamard gate, using elementary CCX gates:
# Synthesize a multi-controlled Hadamard gate (4 control qubits)
circ = QuantumCircuit(8)
circ.ccx(0, 1, 5)
circ.ccx(2, 5, 6)
circ.ccx(3, 6, 7)
circ.ch(7, 4)
circ.ccx(3, 6, 7)
circ.ccx(2, 5, 6)
circ.ccx(0, 1, 5)
circ.draw(output='mpl')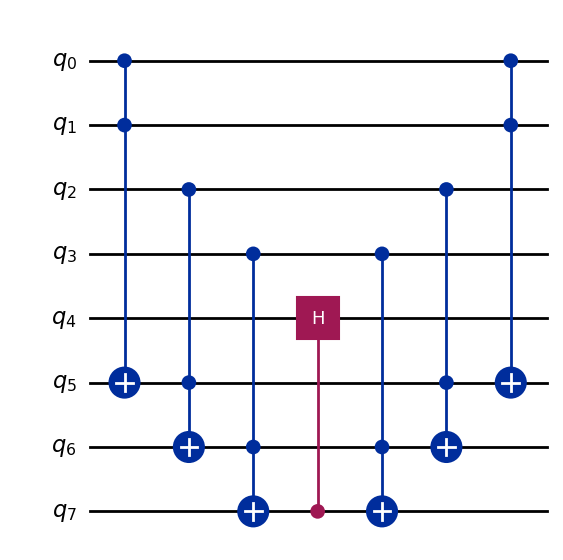
In this circuit, qubits (0, 1, 2, 3) are the control bits and qubit 4 is the target bit. Three ancillary bits (5, 6, 7) are also required for this implementation. The first three CCX gates implement the AND logic that sets qubit 7 to the value 1, only if control bits (0, 1, 2) are all set. The last three CCX gates uncompute the AND logic, to clean up the ancillary bits.
This is the simplest approach to implementing a multi-controlled gate,
but it also requires numerous ancillary bits: requiring m-1 ancillary bits for m control bits.
There are more sophisticated ways of
implementing a multi-controlled gate that do not require any
ancillaries, but these algorithms are much more complicated and
constitute an entire field of research in their own right. This might be
a topic for a future blog post.